|
|
| We are created to do good. |
 |
|
 |
음파의 성질 및 음파에 의해서 생기는 음향현상의 기초를 연구하는 학문으로 음향학의 기원은 동양에서는 중국의 춘추시대, 서양에서는 고대 그리스에서 주로 음악을 위해서 연구되었다. 그러나 과학으로서의 연구가 시작된 것은 갈릴레이나 뉴턴이 진동체의 이론이나 음속을 연구한 17세기경부터라고 할 수 있다.
그 후 해부학의 발달에 따른 청각(聽覺) 연구의 진보와 더불어 미적분학을 이용한 음파의 이론적인 연구가 발전하고, 19세기에 이르러 J.W.S. 레일리와 H.L.F. 헬름홀츠 등에 의해서 기초이론이 체계화되었다.
그러나 이러한 이론들이 응용면과 관련을 가지면서 한층 진전된 것은 20세기에 들어선 후이며, 특히 진공관의 발명에서 비롯되는 전자공학의 발전은 음향학의 진보를 촉진하였고, 정밀한 음향측정에 의거하는 새로운 음향학의 과제를 제출 하였으며, 그와 동시에 갖가지 전기 음향장치를 개발해냈다. 그리고 전기음향학, 건축음향학 ,음향심리학 등 제각기 독자적인 영역을 가지는 관련 부문이 탄생하였으며, 이들의 기초이론으로서 음향학에 대한 연구가 진전되고 있다.
|
 |
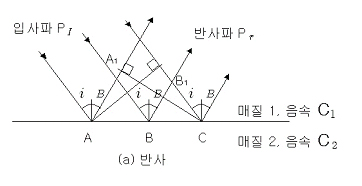
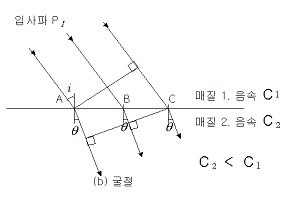
빛이 수면에 입사하면 빛은 일부가 반사하고 나머지는 굴절하여 수중으로 입사하는 것은 잘 알고 있는 사실이다. 초음파의 경우에도 빛과 동일한 현상이 생기고 (1-1) 식의 스넬법칙에 따른다. 지금 그림1에 나타낸 것처럼 매질 1의 음속 C1이 매질 2의 음속 C2보다 큰 2개의 매질이 평면적으로 접하고 있고 매질 1속을 진행하여 온 초음파빔이 경계면에 비스듬히 입사하여 매질 1속에 반사파를, 매질 2속에 굴절파를 생성하는 경우를 생각해 보면 입사파의 음압을 PI, 입사각을 i, 반사파의 음압을 Pr, 반사각을 B, 굴절파의 음압을 Pt , 굴절각을 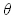 로 나타내기로 한다. 로 나타내기로 한다. |
 |
 |
| <그림1> |
|
그림1에 있어 입사파가 경계면으로 비스듬히 입사할 때 초음파빔에는 폭이 있기 때문에 빔내의 각 부분이 경계면으로 입사하는 위치를 A, B, C로 하면 이러한 점들에 있어 초음파의 도착시각이 각기 다르다. 각점은 초음파가 입사하면 사방으로 초음파를 방사하는 작은 음원이 있는 것과 같은 동작을 나타낸다. 또 각점에서 방사된 초음파의 전달속도는 각 매질 속에서의 초음파 음속과 같다. 경계면에서 매질 1의 내부로 전달되는 초음파에 주목하고 초음파가 C점에 도착한 시각에 있어서의 초음파 선단(파면)위치를 조사하여 보자. A점에는 t초전에 초음파가 도착하고 있으므로 A점에 있는 작은 음원에서 매질 1속으로 방사된 초음파의 선단은 l1=C1t를 반경으로 하는 반원의 위치에 도달하고 있다. B점에는 t/2초전에 초음파가 도착하고 있으므로 B점에 있는 작은 음원에서 매질 1속으로 방사된 초음파의 선단은 l2/2=C1t/2를 반경으로 하는 반원의 위치에 도달하고 있다. 따라서 초음파빔 전체의 선단은 A점을 중심으로 하는 반원, B점을 중심으로 하는 반원의 공통접선 위치에 도달하고 있고 반사원의 파면을 나타내고 있다. 파면상의 접점을 A1, B1으로 하면 반사원의 진행방향은 AA1 및 BB1과 평행한 방향이 된다. 다음에 경계면에서 매질 2의 내부로 전달되는 초음파에 주목하고 초음파가 C점에 도착한 시각에 있어서의 초음파 선단(파면)위치를 조사하여 본다. A점에는 t초전에 초음파가 도착하고 있으므로 A점에서 매질 2 속으로 방사된 초음파의 선단은 l2=C2t를 반경으로 하는 반원의 위치에 도달하고 있다. B점에는 t/2초전에 초음파가 도착하고 있으므로 B점에 있는 작은 음원에서 매질 2속으로 방사된 초음파의 선단은 l2/2=C2t/2를 반경으로 하는 반원의 위치에 도달하고 있다. 따라서 초음파빔 전체의 선단은 반원군의 공통 접선 위치에 도달하고 있고 굴절파의 파면을 나타내고 있다. 파면상의 접점을 A2, B2로 하면 반사원의 진행방향은 AA2 및 BB2와 평행한 방향이 된다.
그림에 있어서 경계면 위의 A점에서 매질 1속으로의 진행거리 l1 및 매질 2속으로의 진행거리 l2는 l1=C1t, l2=C2t가 되고 다음 식을 얻을 수 있다. |
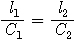 |
| 또 직각삼각형 AA1C와 직각삼각형 AA2C에 있어서 AC가 두 삼각형에 공통이기 때문에 다음 식이 성립된다. |
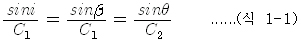 |
이것을 스넬법칙이라 하고 입사각 i, 반사각 B, 굴절각 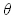 와 음속 C1, C2의 관계는 모두 이식으로 나타낼 수 있다. 매질 2의 음속 C2 가 매질 1의 음속 C1보다 클 때 입사각 i 를 늘리면 굴절각 와 음속 C1, C2의 관계는 모두 이식으로 나타낼 수 있다. 매질 2의 음속 C2 가 매질 1의 음속 C1보다 클 때 입사각 i 를 늘리면 굴절각 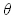 는 는 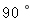 가 된다. 이 때 i 를 임계각이라 하고 이것 이상의 입사각에서는 굴절각은 존재하지 않고 모두 반사해 버린다. 이 현상을 전반사라고 한다. 가 된다. 이 때 i 를 임계각이라 하고 이것 이상의 입사각에서는 굴절각은 존재하지 않고 모두 반사해 버린다. 이 현상을 전반사라고 한다. |
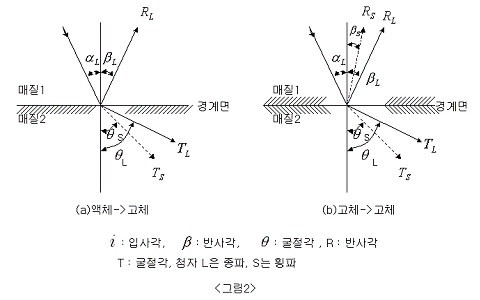 |
| 그림2에 액체와 고체 및 고체와 고체의 경계면에 있어서의 입사시 반사 및 굴절을 나타낸다. 이러한 것은 모두 (1-1)식으로 표현할 수 있다. 그리고 그림2 및 (1-1)식에서 알 수 있는 것처럼 종파가 경계면으로 비스듬히 입사(경사입사)했을 때 반사굴절에 따라 종파의 일부가 횡파로 변환된다. 이 같은 경우 모드변환(파형변환)에 의해 횡파가 발생했다고 한다. |
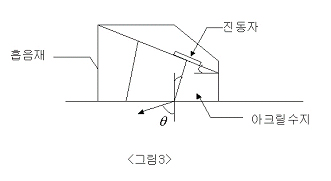 |
| <그림3>은 사각탐촉자의 단면도이다. 아크릴수지 속을 전달하여 온 종파의 초음파는 강철 속으로 입사하여 굴절통과 했을 때 모드변환에 의해 강철 속에서는 횡파의 초음파가 전달되고 있다. 사각탐촉자에서 강재 속에 횡파만을 전달시키기 위해서는 아크릴 수지의 쐐기 각도범위를 어느 정도로 하면 좋은가를 구해야 한다. 여기서 강재 속의 종파음속 CL은 5900m/s, 횡파음속 CS는 3230m/s이며 또 아크릴 수지의 쐐기각도 i 는 입사각 i 와같다. 또 강재 속에 횡파만을 전달시키기 위해서는 굴절종파가 나오지 않도록 즉 굴절종파에 대한 임계각 iLC 이상으로 또 굴절횡파가 나오도록 즉, 굴절횡파에 대한 임계각 iSC미만이 되도록 조정해야 한다. 임계각 iLC를 (1-1)식에 대입하면 다음의 관계가 성립한다. |
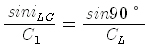 |
| (여기서 C1은 아크릴 수지 내에서의 종파속도)이식을 변형하여 임계각을 구하면 다음과 같이 된다. |
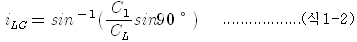
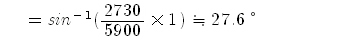
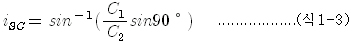
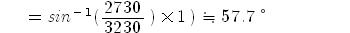 |
따라서 입사각이 |
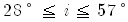 |
가 되도록 쇄기의 각도 i 를 가공하면 된다. 또 이 입사각 i
의 범위에 있어서 횡파굴절각  S의 범위는 (1-1)식을 변형하여 다음과 같이 구할 수 있다. S의 범위는 (1-1)식을 변형하여 다음과 같이 구할 수 있다. |
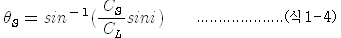
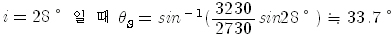
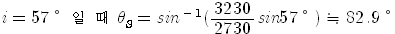 |
따라서 횡파의 굴절각 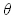 S는 S는 |
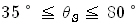 |
| 가 된다. 보통 초음파 탐상시험에 이용되고 있는 사각탐촉자의 굴절각은 |
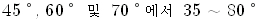 |
| 의 범위가 포함되고 이러한 탐촉자를 이용하는 경우 강철 속에서는 횡파만이 전달되고 종파는 전달되지 않는다. |
|
|
|
|
|

